Refactoring - Part V

Backtester Interfaces: Commission & Funding

Table Of Contents

• Recap

• Trading Isn't Free

• Fees Design

• Fees assert() Calls

• Fees Implementation

• Calculating Post-Cost SR Design

• The Fee Strategy

• Holding Costs Design & Implementation

It's been a few weeks since the last article. Sorry about that; life's been busy! To avoid staying radio silent any longer, I'm going to take this one right here out of draft mode and cut it short. It's not all the way down to the post-cost SR as promised but I'll pick it up and finish it next time.

Recap

In our last article we finished migrating the pre-cost SR calculation to our new interface-focused backtester. During this we found a bug and fixed it, for which we had to pay 0.3 of annual SR units.

Today we're going to continue the process of porting over implementations from our old backtester until we finally have our new one spit out a post-cost SR calculation again. The only thing really missing are the cost calculations to deduct from our pre-cost SR.

Let's get going!

Trading Isn't Free

As already stated earlier, we can't trade for free. To be able to trade we need to pay a whole bunch of different costs, which is why we made it a pillar in our 4 F's of backtesting

One of the most obvious costs are commissions and holding costs.

Fees Design

The commissions - often also referred to as just "fees" - we have to pay depend on the venue we're trading at. Since in our example we're still assuming to execute on ByBit, we have to calculate the fees paid based on their fee structure for perpetual & futures contracts, which is basically just a percentage cut of our notional traded.

The current design for the calculation looks like this:

1. Get fee rate for instrument type (perps) and order type (market-order = taker)

2. Convert to decimal if needed (/100)

3. Calculate the notional traded for each day

   • diff between ideal_pos_contracts and current_pos_contracts if diff > rebalance_threshold

   • notional_traded = (contract_diff x close x contract_unit)

4. fees paid = multiply notional_traded x exchange_fee_dec

5. Deduct fees from PNL

Obviously this is still very specific to our current use case of trading crypto perpetuals on ByBit. Some exchanges will charge you in the form of percentage fees, some others will charge a fixed amount per contract, etc.

Although we want to focus on reusability of our code with composition in mind to prepare for future changes, I think it's not worth it right now to research the fee structure for lots of exchanges and build the implementations for them. We'll come to this when we tackle fetching live (and historical) price data from different venues, giving them some more well-rounded places to live in. Our main focus is to port over the current implementation into our new backtester and get the correct asserts in place for it.

Fees assert() Calls

We can prepare by thinking about some assert() calls that might make sense for commissions. However, there's not a whole lot we can do right now to do both: validating the current implementation after migration to the new backtester while ALSO keeping it very generic so we can use it for other implementations in the future.

There are some general checks we can use to get some sense of sanity while working on our code, though. First we can check if the fees calculated make sense at all. For example fees shouldn't be below 0 if we trade. They should also be a number, and zero contracts traded should result in 0 fees. And of course our check if everything is working like before:

total_fees_paid = fees_paid_series.sum()

print("\n")

print("Testing trading costs...")

print("Testing fee structure...")
assert total_fees_paid > 0, "Total fees should be positive"
assert isinstance(total_fees_paid, float), "Fees should be float values"

zero_trade_mask = contracts_traded == 0
assert (fees_paid_series[zero_trade_mask] == 0).all(), "Zero trades should result in zero fees"

assert (total_fees_paid == 1038.6238698915147)

Since this is a percentage-based calculation, we can simply check if it works like this:

assert (total_fees_paid == notional_traded.sum() * FEE_PERCENT / 100)

Fees Implementation

Here's our current implementation and usage:

def calculate_notional_percentage_fees(fee_percentage, notional_traded):
    fee_decimal = fee_percentage / 100
    return (notional_traded * fee_decimal).fillna(0)

# Usage
contracts_traded = abs(rebalanced_positions.diff()).fillna(0)

FEE_PERCENT = 0.055  # ByBit's fee rate
notional_traded = instrument.get_feature('close') * contracts_traded * instrument.contract_unit

fees_paid_series = calculate_notional_percentage_fees(FEE_PERCENT, notional_traded)

total_fees_paid = fees_paid_series.sum()
print(f"Total fees paid: {total_fees_paid:.2f}")

This is already designed based on our top-level use-case of calculating the post-cost SR (see next paragraph) so we can easily swap it out later for some other structure like fixed amount per contract:

Calculating Post-Cost SR Design

1. Calculate pre-cost SR

2. Calculate fees paid, deduct from pre-cost SR

3. Calculate holding costs, deduct from pre-cost SR

4. Calculate slippage, deduct from pre-cost SR

5. Calculate bid-ask spread, deduct from pre-cost SR

Each step here is defined generic. They don't hold any information about how to achieve their goal and leave room for either improvements or swapping current implementations out for more sophisticated ones. We could use multiple different fee structures while still talking to the same interface. We could improve our current slippage-model to estimate based on rolling volatility instead of hardcoding a historical average, etc.

The Fee Strategy

Let's take a look at a concrete example on how to make use of this design approach. By using the so-called Strategy Pattern we can specify a generic interface to rely on and then use Indirection to forward the responsibility of actually calculating the fees. By reversing the responsibilities, we rid our post-cost SR design of any implementation details regarding fees. The strategy pattern is a common pattern used to achieve modularity. We're going to use it a lot throughout our first iterations; in fact, we're going to use it every time until we reach its limits.

Our backtester will become a pretty generic sequence of steps agnostic of implementation so we can run a lot of different trading strategies through it quickly, hot-swapping stuff here and there as we see fit. Whenever we have a new algorithm for something, we can just switch it with the current (read: outdated) version.

from fees import FeeCalculation

# leveraging indirection on fee_strategy
def calculate_postcost_sr(pre_cost_sr, fee_strategy: FeeCalculation):
    fees_paid_series = fee_strategy.calculate_fees()
    # deduct fees from pre-cost SR (vol adjusted)
    # return post_cost_sr
    pass

# Two types of fee calculations: Notional percentage vs. Fixed amt. per contract
from abc import ABC, abstractmethod

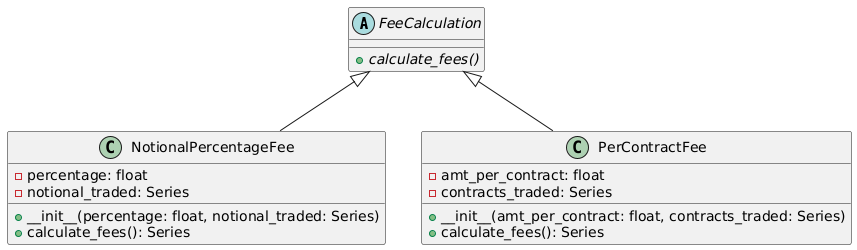
class FeeCalculation(ABC):
    @abstractmethod
    def calculate_fees(self):
        pass

class NotionalPercentageFee(FeeCalculation):
    def __init__(self, percentage, notional_traded):
        self.percentage = percentage
        self.notional_traded = notional_traded

    def calculate_fees(self):
        return self.notional_traded * (self.percentage / 100)

class PerContractFee(FeeCalculation):
    def __init__(self, amt_per_contract, contracts_traded):
        self.amt_per_contract = amt_per_contract
        self.contracts_traded = contracts_traded

    def calculate_fees(self):
        return self.amt_per_contract * self.contracts_traded

Here it is as UML diagram, both strategies have the same method calculate_fees() but different underlying structure.

And here's how to use both in isolation:

from fees import NotionalPercentageFee

FEE_PERCENT = 0.055  # ByBit's fee rate %
notional_traded = instrument.get_feature('close') * contracts_traded * instrument.contract_unit

perc_fee_calculator = NotionalPercentageFee(FEE_PERCENT, notional_traded)
fees_paid_series = perc_fee_calculator.calculate_fees()
total_fees_paid = fees_paid_series.sum()

# OR
from fees import PerContractFee

fee_per_contract = 0.50  # in USD

fixed_fee_calculator = PerContractFee(fee_per_contract, contracts_traded)
fees_paid_series = fixed_fee_calculator.calculate_fees()
total_fees_paid = fees_paid_series.sum()

And here's how to use it leveraging the strategy indirection:

# Setting up notional percentage fees
contracts_traded = abs(rebalanced_positions.diff()).fillna(0)

FEE_PERCENT = 0.055  # ByBit's fee rate
notional_traded = instrument.get_feature('close') * contracts_traded * instrument.contract_unit

from fees import NotionalPercentageFee
notional_perc_fee = NotionalPercentageFee(FEE_PERCENT, notional_traded)



# Setting up fixed USD amount per contract fee
fee_per_contract = 0.50  # in USD

from fees import PerContractFee
fixed_contract_fee = PerContractFee(fee_per_contract, contracts_traded)



# Using them
pre_cost_sr = 1.678


post_cost_sr = calculate_postcost_sr(pre_cost_sr, notional_perc_fee)

# OR
post_cost_sr = calculate_postcost_sr(pre_cost_sr, fixed_contract_fee)

Passing in either of them works because the calculate_postcost_sr() function does not care about the exact implementation details. It only cares about its interface - which we defined in fees.py as FeeCalculation::calculate_fees()

Holding Costs Design & Implementation

Unfortunately, commissions are not the only "fees" we have to pay. From our post-cost SR design - Step 3 - we can see that there's also something called holding costs associated with trading activity. Holding costs can take many different forms but in our case, since we're trading crypto perps, our holding costs are called funding.

To reiterate what funding is all about, an excerpt from our first backtest article:

"When the index price is above your contracts mark price, funding is negative and longs get paid. If it's the other way around - index < mark - funding is positive and shorts get paid. The wider the difference between index and mark, the higher the funding.

The current design looks like this:

1. Get funding fee structure for instrument on exchange

   • in our case % of notional position every X hours

2. Fetch historical funding fees

3. Resample the fee structure to trading period (24h)

4. Calculate daily notional_pos (rebalanced_pos_contracts x notional_per_contract)

5. Multiply notional position series with resampled funding series

6. Deduct from PNL

Since we might want to trade different instruments with different holding cost structure in the future, we can use the strategy pattern again. We should do the same for the funding data fetching mechanism. Right now funding data is read from a .csv file but we also want to be able to read it from a database. I'm going to skip the details for now because it's basically the same thing as we did with commissions and funding while also leveraging the CSVReader and DBReader we created a while back.

We can use the same set of assert() calls as for the fees paid:

assert total_funding_paid > 0, "Total funding paid should be positive"
assert isinstance(total_funding_paid, float), "Total funding paid should be a float"

zero_position_mask = notional_positions[common_dates] == 0
mismatched_entries = funding_paid[zero_position_mask][funding_paid[zero_position_mask] != 0]

if not mismatched_entries.empty:
    print("\nFound non-zero funding paid for zero positions:")
    for date, value in mismatched_entries.items():
        print(f"Date: {date}, Funding paid: {value:.8f}")
    assert False, f"Found {len(mismatched_entries)} cases where zero positions had non-zero funding"

assert (total_funding_paid == 3130.3644113437113), f"Total funding paid {total_funding_paid} does not match expected value."

If we run this, we get AssertionError: Total funding paid 3132.8033950021845 does not match expected value. This is correct because we asserted the funding to be paid to be assert (total_funding_paid == 3130.3644113437113). But why?

First of all, this looks kind of neglectable. It's a difference of 0.078%! But if we look at the old backtest.py we can see that we're calculating the funding paid via df['funding_paid'] = df['ideal_pos_notional'].shift(1) * df['funding']. This is obviously nonsense because we don't always have the ideal position on. We iterated from always (daily) rebalancing towards only rebalancing if our positions exceeds the 10% error threshold. But we forgot to reflect that in our funding fee calculations. Let's update the old backtest.py accordingly and port over the new values into our assert() calls to sync them again: df['funding_paid'] = df['rebalanced_pos_contracts'].shift(1) * df['notional_per_contract'] * df['funding']

Now that we've established a correct test-case again, we can start implementing our strategy pattern. If we weren't trading perps but futures contracts that expire, we'd be forced to close our position on expiry and open the same position in the next contract. This is called rolling; see more info here

This is where I'm cutting the article short tho.

We're going to continue with the RollingStrategy next time and also port over Slippage and Bid-Ask Spread to then finally have a working post-cost SR calc again.

The full code for this article can be found here

So long, happy trading!

- Hōrōshi バガボンド

Disclaimer: The content and information provided by Vagabond Research, including all other materials, are for educational and informational purposes only and should not be considered financial advice or a recommendation to buy or sell any type of security or investment. Vagabond Research and its members are not currently regulated or authorised by the FCA, SEC, CFTC, or any other regulatory body to give investment advide. Always conduct your own research and consult with a licensed financial professional before making investment decisions. Trading and investing can involve significant risk, and you should understand these risks before making any financial decisions. Backtested and actual historic results are no guarantee of future performance. Use of the material presented is entirely at your own risk.